Implementace principu kytarové ladičky na signálovém procesoru

Zkusíme navrhnout algoritmus pro implementaci principu kytarové ladičky do signálového procesoru TMS320C54x. Vstupem bude záznam zvukového signálu ladění kytarové struny E6. Výstupem bude signál s intenzitou odpovídající shodě vstupní frekvence s referenční (správnou) frekvencí 83 Hz.
Tip: Pokud máte elektrickou kytaru nebo basovku a chcete ji připojit do zesilovače, pak si u nás můžete vybrat také nějaký kytarový kabel.
Teoretický úvod
Kytara, jak známo, má 6 strun. Frekvence tónů jednotlivých strun jsou poměrně nízké a i při uvažování vyšších harmonických není nijak náročné její zvuk číslicově zpracovávat. Frekvence strun jsou následující:
| Struna | Frekvence [Hz] |
|---|---|
| E6 | 82.41 |
| A5 | 110.00 |
| D4 | 146.83 |
| G3 | 196.00 |
| B2 | 246.94 |
| E1 | 329.63 |
Kytarové elektronické ladičky většinou fungují tak, že ze vstupního signálu (mikrofonu) automaticky detekují nejsilnější tón a zobrazují odchylku od správné frekvence, na kterou se má struna naladit. Dokonalejší ladičky umí detekovat jakýkoliv tón v rozsahu několika oktáv a uživatel je může podle potřeby i překalibrovat až o půl tónu.
Možnosti detekce tónu
Nabízejí se dvě základní metody pro detekci tónu:
Ve frekvenční oblasti: z dostatečně dlouhé posloupnosti vstupních vzorků se vypočítá FFT, následně se určí nejvýraznější frekvence, k ní se vypočítá nejbližší referenční tón a určí se odchylka od reference. Při měření je vhodné provádět průměrování, aby se odstranil vliv šumu.
V časové oblasti: pomocí adaptivního filtru – viz dále.
Adaptivní filtrace
Princip adaptivního filtru je následující:
Koeficienty adaptivního filtru jsou proměnlivé v čase za účelem optimalizace daného požadavku.
Nejčastěji používaným algoritmem pro adaptaci koeficientů je LMS (Least Mean Square).
Filtry jsou nejčastěji FIR z důvodu stability.
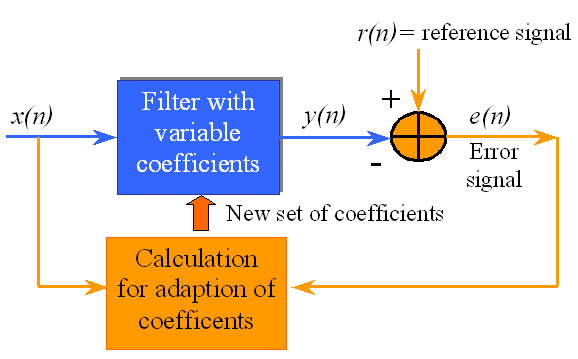
Algoritmus LMS
Pro každý vzorek:
Filtr filtruje vstupní signál pomocí variabilních koeficientů bi.
Podle chybové funkce upraví koeficienty bi.
Přesnost konvergence filtru závisí na:
Adaptačním kroku δ: čím vyšší δ, tím rychleji filtr konverguje, ale s nižší přesností.
Počtu koeficientů N: zbytková chyba je úměrná počtu koeficientů N, tedy řádu filtru.
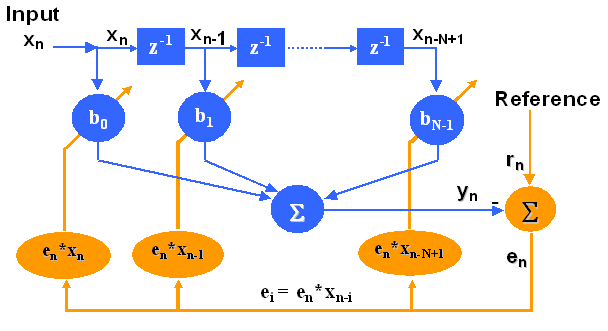
Podstata algoritmu LMS
-
Pro každý vzorek:
Spočítá chybu: en=rn-yn
Váhuje chybu adaptačním krokem δ: en'= δ·en
-
Pro každý vzorek a každý koeficient:
Pronásobení váhované chyby a signálu: ei=en' · xn-i
Násobení xn-i · bi a akumulace
Výpočet nových koeficientů: novýbi=bi+ei
Aktualizace koeficientů: bi=novýbi
Implementace
Implementaci tohoto algoritmu si ukážeme v jazyce C, v Matlabu a v assembleru.
Adaptivní filtr v jazyce C
Firma Texas Instruments dodává na výukovém CD kompletní program kytarové ladičky v jazyce C napsaný pro vývojovou desku s procesorem TMS320C5416. Pro základní funkci detekce tónu jedné struny stačí převzít minimum. Uvádíme základ algoritmu adaptivní filtrace ze souboru na výukovém CD adaptive_filter.c (s vynecháním některých komentářů z důvodu úspory místa):
#define N 12
#define BETA 5600
static signed int x[N]; /* Array to hold input samples */
static signed int w[N]; /* Weights (adaptive filter coefficients)*/
static signed int error; /* Difference between desired and actual. */
void adaptive_filter_initialize(void)
{
unsigned int i;
for ( i = 0 ; i < N ; i++)
{
w[i] = 0;
x[i] = 0;
}
error = 0;
}
signed int i;
signed long y; /* Output of adaptive filter */
signed long difference;
signed long adaptive_filter( signed int desired, signed int latest_measurement)
{
for ( i = N-1 ; i > 0 ; i--)
{
x[i] = x[i-1];
}
x[0] = latest_measurement;
difference = error * BETA;
error = (signed int) (difference >> 15); /* Update error */
y = 0; /* Start accumulation at zero */
for ( i = N-1 ; i >= 0 ; i--)
{
y += ((long)(x[i] * w[i]) >> 0 ); /* Prevent overflows */
difference = ( (long) error * x[i] ) >> 14;
if ( difference & 0x0001)
{
if ( difference >= 0)
{
difference++ ; /* Round up when above zero */
}
else
{
difference--; /* Round down when below zero */
}
}
w[i] += (signed int) ( difference >> 1);
} // end for
y >>= 15; /* Remove remains of fractional part */
error = desired - (signed int) y;
return( ( y << 16 ) | (long) error ); /* Return y OR error */
}
Simulace adaptivní filtrace v Matlabu
Algoritmus napsaný v jazyce C je celkem snadno pochopitelný. Dále je uveden přepsaný do Matlabu, aby bylo možné ho odsimulovat se skutečným signálem laděné struny E6. Výpis souboru adaptivni_filtr.m:
%%% Adaptive filter
% Definice konstant
% N is number of elements in adaptive filter
N=34; % in C: 12, in ASM: 34
% BETA is the amount of the output used for feedback to determine the new
% filter weights. 56 represents 56/32767 i.e. 0.002
% We could also approximate 0.002 to 1/512 i.e. divide by 2 ^ 9
beta=5600; % in C: 5600, in ASM: 560
L=20000; % delka vzorkovaneho signalu
fs=11025; % [Hz] - vzorkovaci frekvence
fstring=83; % [Hz] - struna E
amp=8191; %8191 - zesileni
%% inicializace
% vnitrni promenne
x_ar=zeros(1,N); % Array to hold input samples
w_ar=zeros(1,N); % Weights (adaptive filter coefficients)
difference=0; % rozdil mezi pozadovanou a skutecnou hodnotou
i=0; % promenna pro cykly
% vystupni promenne
y=0; % vystup filtru
error=0; % Difference between desired and actual.
% vystupni promenne pro plot
y_ar=zeros(1,L);
error_ar=zeros(1,L);
%% Definice poli
desired=sinus(fstring,L,fs).*amp; % vytvoreni referencni frekvence
wavplay(desired./amp,fs);
%% nahraju zvuk
if(0)
zvuk=getsample(L,fs);
zvuk=zvuk.*amp; % normalizace zvuku
else
load zvuk;
zvuk=zvuk.*amp; % normalizace zvuku
wavplay(zvuk./amp,fs);
end;
%% vlastni filtrace
for k=1:L
latest_measurement=zvuk(k);
% posunuti vzorku v pameti filtru; na 1. pozici dosadim aktualni vzorek
for i=N : -1 : 2
x_ar(i)=x_ar(i-1);
end;
x_ar(1)=latest_measurement;
% rozdil
difference = error * beta;
% aktualizace chyby
error=bitshift(difference,-15); %-15
y = 0; % Start accumulation at zero
% FIR filtr
for i=N : -1 : 1
y=y+x_ar(i)*w_ar(i); % nasobeni a akumulace
difference=bitshift(error*x_ar(i),-14); %-14
% Remove fractional part then update coeffient W[i]
if (abs(difference)>=1)%bitand(difference,1)
if ( difference >= 0)
difference=difference+1; % Round up when above zero
else
difference=difference-1; % Round down when below zero
end;
end; % endif
w_ar(i)=w_ar(i)+bitshift(difference,-1); %-1
end; % end for
y=bitshift(y,-15);%-15 % Remove remains of fractional part
error=desired(k)-round(y);
%ret=y*(2^16) + error; % Return y OR error
y_ar(k)=y;
error_ar(k)=error;
end; % end for
%% Vykresleni vysledku
figure(2);
subplot(411);
plot(zvuk);
title 'Vstupni signal';
subplot(412);
specgram(zvuk);
title 'Spektrogram vstupniho signalu';
subplot(413);
plot(y_ar);
title 'Vystup filtru';
subplot(414);
plot(error_ar);
title 'Chybova funkce';
wavplay(y_ar./(amp/8),fs);
wavplay(error_ar./(amp/2),fs);
Funkce getsample.m zajistí nahrání zvuku z mikrofonu připojeného do zvukové karty počítače:
function y=getsample(delkavz,fs)
a=questdlg('Bude se nahravat vzorek. Pripraven?');
if strcmp(a,'Yes')
for i=100000:-1:0
% zpozdovaci odpocitavani - aby byl cas se pripravit
k=i
end;
y = wavrecord(delkavz, fs, 'double'); % Nahrani zaznamu
elseif strcmp(a,'No') % synteticky signal
f=83;
t=1:delkavz;
y=chirp(t , f-1 , delkavz*4 , f+1);
end
figure(1);
subplot(221);
plot(y);
title('Vstupni zvukovy signal');
axis([0 delkavz -1 1]);
subplot(222);
specgram(y);
title('Spektrum vstupniho zvukoveho signalu');
y = normal(y); % Normovani na 1
figure(1);
subplot(223);
plot(y);
axis([0 delkavz -1 1]);
title('Normovany vstupni signal');
subplot(224);
ffty=abs(fft(y));plot(ffty);
axis([0 delkavz/2 0 max(ffty)*0.75]);
title('Spektralni slozky vstupniho signalu');
wavplay(y, fs);
Funkce sinus.m vytvoří sinusový signál o dané frekvenci, počtu vzorků a vzorkovací frekvenci:
function ret=sinus(f,delkavz,fs)
t=1:delkavz; % casova osa
ret=sin(2*pi*t*f/fs);
Výsledky simulace
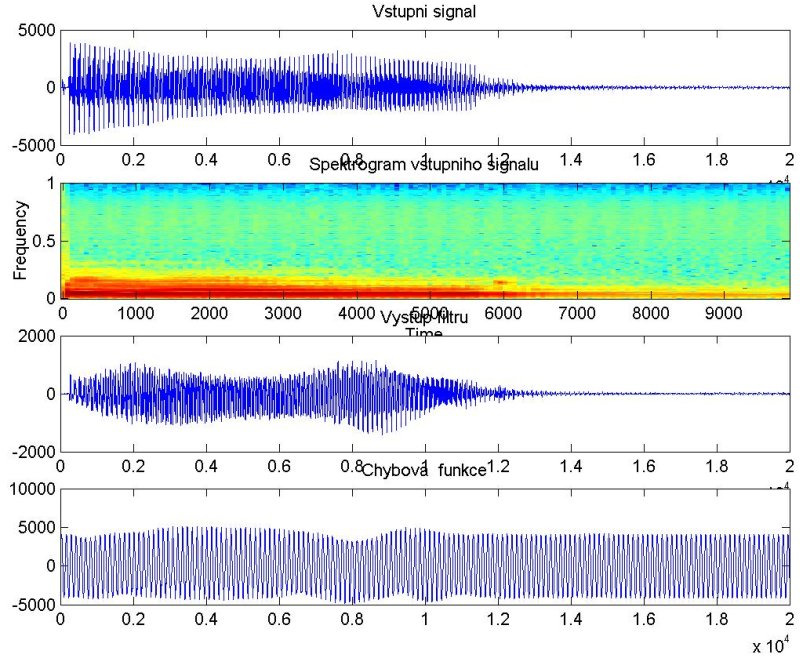
Během doznívání tónu kytary by se adaptivní filtr měl naladit na frekvenci 83 Hz a chybová funkce by měla konvergovat k nule.
Implementace v assembleru procesoru TMS320C5416
Uvádíme zde přepis algoritmu adaptivního filtru do assembleru, který jsme s úpravami převzali rovněž z výukového CD firmy Texas Instruments. Některé komentáře jsou z důvodu úspory místa vynechány.
.mmregs
FP .set AR7
; Number of elements in filter X[]
;#define N 12
N .set 34
; Feedback amount. Affects convergence rate of filter.
;#define BETA 5600
BETA .set 560
; Storage on stack
INPUT .set 9
; Variables used in function
;static signed int x[N]; /* Array to hold input samples */
.bss _X_1,N,0,0
.bss _X_2,N,0,0
;static signed int w[N]; /* Weights (adaptive filter coefficients)*/
.bss _W_1,N,0,0
.bss _W_2,N,0,0
;static signed int error; /* Difference between desired and actual. */
.bss _error_1,1,0,0
.bss _error_2,1,0,0
.bss _desired,1,0,0
; Functions callable from C code
.sect ".text"
.global _adaptive_filters_asm_initialise
.global _adaptive_filter_asm_1
.global _adaptive_filter_asm_2
;void adaptive_filter_initialize(void)
;{
_adaptive_filters_asm_initialise:
; unsigned int i;
PSHM AR3 ; Keep original value of AR3 - push into stack
; for ( i = 0 ; i < N ; i++)
; {
LD #0, A ; Clear accumulator A
; w[i] = 0;
STM #_W_1, AR3
RPT #(N-2)
STL A, *AR3+ ; Fill Weights with zeroes
STM #_W_2, AR3
RPT #(N-2)
STL A, *AR3+ ; Fill Weights with zeroes
; x[i] = 0;
STM #_X_1, AR3
RPTZ A, #(N-2) ; Fill 0 to N-1. Less one for repeats
STL A, *AR3+ ; Fill X array with zeroes
STM #_X_2, AR3
RPTZ A, #(N-2) ; Fill 0 to N-1. Less one for repeats
STL A, *AR3+ ; Fill X array with zeroes
; }
; error = 0;
STL A, *(_error_1) ; Clear errors to zero
STL A, *(_error_2)
;}
POPM AR3 ; Restore original value of AR3
FRET ; Far return
; 1st parameter in accumulator = desired (or reference) waveform.
; 2nd parameter on stack = input signal (unknown) to be compared with the reference.
; Desired is copied from accumulator A to stack frame.
; Returns Y in AH, error in AL
; RETURNS: Filter output y in high word. Error in low word
;signed int i;
;signed long y; /* Output of adaptive filter */
;signed long difference;
;signed long adaptive_filter( signed int desired, signed int latest_measurement)
;{
_adaptive_filter_asm_1:
PSHM ST0 ; Keep original values of flags
PSHM ST1
PSHM AR3 ; Keep original values of auxiliary registers
PSHM AR4
FRAME #-3 ; Setup stack frame
SSBX SXM ; Turn on sign-extension mode
SSBX FRCT ; Extra shift for multiplications
SSBX OVM ; Prevent overflow
LD #0, ASM ; Required for correct behaviour of ST || MPY
; nulovy bitovy posun
STL A, *(_desired) ; Copy desired from Accumulatr A to local storage
STM #(_X_1 + N-2), AR3 ; AR3 points to X[N-2]
; /* Shuffle first and update */
; for ( i = N-1 ; i > 0 ; i--)
; {
; x[i] = x[i-1];
; }
RPT #(N-1-1)
DELAY *AR3- ; Shuffle values along one place
MVDK *SP(INPUT), *(_X_1); Copy in latest value to X[0]
LD *(_error_1), T ; T = error
MPY #BETA, A ; A = error * BETA
SFTA A, -16, A ; Move AH to AL
STLM A, T ; T = error * BETA
; Setup pointers to X[0] and W[0]
STM #(_X_1), AR3 ; AR3 points to X[0]
STM #(_W_1), AR4 ; AR4 points to W[0]
SUB B, B ; Clear accumulator B
MPY *AR3, A ; A = error * BETA * X[]
; Perform Least Mean Squares calculations.
STM #(N-1), BRC ; Set number of block repeats
RPTB end_lms_1 - 1 ; Repeat instructions up to end_lms
LMS *AR4, *AR3+ ; A = W[] + error * BETA * X[]
; B += W[] * X[]
ST A, *AR4+ ; Update W[]. Point to next W[]
|| MPY *AR3, A ; Last multiply is ignored
end_lms_1:
; Build up return value of output of filter Y in AH and error in AL
LD B, -16, A ; BH = Y. Copy Y to AL
NEG A ; A = (-Y)
ADD *(_desired), A ; AL = Desired + (-Y) = error
STL A, *(_error_1) ; Save error for next time through
PSHM BH ; Copy Y in BH to AH
POPM AH ; Combined return value. AH = Y. AL = error
FRAME #3 ; Restore stack frame
POPM AR4 ; Restore auxiliary registers
POPM AR3
POPM ST1 ; Restore FRCT, SXM, OVM, C
POPM ST0
FRET ; Far return
Použitá literatura
[1] Davídek, V., Sovka, P.: Číslicové zpracování signálů a implementace, Vydavatelství ČVUT, 2002
[2] Výukové CD „C5000 Teaching ROM“, Texas Instruments, 2003
[3] TMS320C54x DSP – Reference Set – Volume 2: Mnemonic Instruction Set, Texas Instruments, 2001 (SPRU172C.pdf)
