1. Teoretický úvod
1.1. Zvukový efekt Tape delay
Tape Delay je zvukový efekt, který byl hodně používán zejména v 80. letech 20. století v popové a rockové hudbě. Jeho princip naznačuje následující schéma:
Obr.1: Princip hudebního efektu Tape Delay
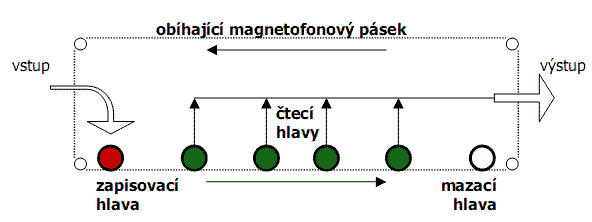
Signál je přiváděn na zapisovací magnetofonovou hlavu, která ho zaznamená na pásek pohybující se konstantní rychlostí. S definovaným zpožděním je signál znovu opakovaně přečten několika čtecími hlavami a zeslaben v daném poměru. Aby nedocházelo ke kladné zpětné vazbě, musí být následně smazán mazací hlavou. Zvuk, který projde tímto efektem, se pak jeví např. jako ozvěna v tunelu.
1.2. Převzorkování
Systémy s převzorkovámím jsou velmi rozšířené a velmi usnadňují zpracování signálů i jeho implementaci.
Převzorkováním se rozumí změna vzorkovací frekvence. Pro snížení vzorkovací frekvence používáme decimaci, pro zvýšení interpolaci. Použití převzorkování bývá motivováno např. těmito důvody:
-
Zvýšením vzorkovací frekvence výrazně nad Nyquistovu frekvenci zvětšujeme efektivní šířku přechodového pásma, čímž můžeme výrazně zjednodušit návrh analogových omezovacích filtrů.
-
Snížením vzorkovací frekvence měníme mezní frekvenci číslicových filtrů a šířky přechodových pásem. Tím klesá řád filtru a paměťové nároky filtru a snižuje se riziko jeho nestability.
-
Převzorkované signály obsahují redundance, které lze využít k redukci efektů náhodných chyb.
-
Zvýšení vzorkovací frekvence – interpolace – dovoluje snižovat nároky na rekonstrukční analogové filtry.
-
Decimací a interpolací lze významně snížit počet aritmetických operací a tedy i výpočetní nároky číslicových systémů pracujících v reálném čase, kdy tyto systémy musí všechny operace vykonat během jedné periody.
1.2.1. Decimace
Decimace je snížení vzorkovacího kmitočtu v celočíselném poměru M. Musí jí předcházet antialiasingový filtr, který zamezí překrývání spekter na nižších kmitočtech a vybere z celého spektra pouze signál do frekvence fnyq/M, kde fnyq=fs/2 je Nyquistova frekvence, tedy polovina vzorkovacího kmitočtu. Decimace s faktorem M spočívá ve vynechání M-1 vzorků z M vzorků filtrovaného signálu w[n].
Matematicky lze popsat vztah mezi vstupními a výstupními vzorky takto:
y[M] = w[mM] = ∑k=-∞∞ h[k] x[mM-k],
kde je w[m] = ∑k=-∞∞ h[k] x[m-k]
Tomu odpovídá následující schéma:
Obr.2: Schéma decimace
Pokud jsou požadovány velké změny vzorkovací frekvence, bývá účinnější změnit frekvenci ve více krocích postupnou decimací.V praktických systémech bývá tato postupná změna aplikována často, neboť vede na značné snížení požadavků na filtry a tudíž i ke snížení nároků na paměť. V tom případě postupujeme od nejvyššího decimačního faktoru k nejnižšímu. Jako optimální se zpravidla jeví používání dvou- až tříkrokové decimace.
V Matlabu máme k dispozici funkci y=decimate(x,M), která používá pro omezení spektra Čebyševovu dolní propust 8. řádu s mezní frekvencí 0,4fs/M.
1.2.2. Interpolace
Interpolace je zvýšení vzorkovací frekvence v celočíselném poměru L. Interpolátor s faktorem L vkládá mezi jednotlivé vzorky signálu x[n] L-1 vzorků s nulovou hodnotou a vytváří tak nový signál se vzorkovacím kmitočtem Lfs.
Takto lze interpolaci popsat matematicky:
y[m] = ∑k=-∞∞ h[k] w[m-k],
kde je:
w[m] = x[m/L] pro m=0, ±L, ±2L atd.;
0 jinde.
Při interpolaci se generují nové obrazy spektra ve frekvenční oblasti. Proto je nutno použití filtrace. Filtrujeme-li signál s vloženými nulami dolní propustí s mezní frekvencí fnyq/L, pak odstraníme obrazy frekvenčního spektra vzniklé vložením nul. Na výstupu dolní propusti získáme interpolovaný signál y[m]. Vložení L-1 nul rozprostře energii vzorků signálu na L výstupních vzorků, což musíme kompenzovat násobením vzorků y[m] činitelem L.
Následující schéma popisuje proces interpolace:
Obr.3: Schéma interpolace
Pro velké změny vzorkovací frekvence provádíme postupnou interpolaci. Platí zde podobné závěry jako při decimaci: Jako optimální se jeví použití dvou- až tříkrokové interpolace. Postupujeme od nejnižšího interpolačního faktoru k nejvyššímu.
V Matlabu lze použít funkci y=interp(x,L), která rozšíří vstupní posloupnost x[n] vložením L-1 nul mezi původní vzorky. Ve funkci je implementován dolnopropustní FIR filtr o délce 8L+1.
1.2.3. Změna kmitočtu v neceločíselném poměru
V této úloze se mimo jiné zaměříme na změnu kmitočtu v neceločíselném poměru. Toho dosáhneme postupným uplatněním interpolace a decimace, jak ukazuje následující schéma:
Obr.4: Změna kmitočtu v neceločíselném poměru
Je třeba, aby interpolace předcházela decimaci, neboť decimace by mohla odstranit požadované frekvenční složky spektra.
Abychom se vyhnuli příliš velikým vzorkovacím kmitočtům po interpolaci, můžeme zkombinovat vícekrokovou interpolaci a decimaci. V každém kroku provedeme interpolaci, filtraci a decimaci faktory, které jsou celočíselnými zlomky celkových faktorů interpolace L a decimace M. Navíc můžeme v každém kroku ušetřit jeden filtr tím, že vložíme jednu dolní propust mezi interpolátor a decimátor.
Pro převzorkování můžeme v Matlabu použít funkci y=resample(x,L,M). Tato funkce obsahuje dolnoprpustný antialiasingový FIR filtr a zároveň má kompenzaci zpoždění signálu.
1.3. Chromatická hudební stupnice
Připomeňme, jakým způsobem se stupnice tvoří. Máme-li jeden vztažný tón o frekvenci f0, pak frekvence tónů následujících jsou od sebe vzdáleny vždy násobkem koeficientu 12√2, tedy:
fi = 12√2i · f0 = 2i/12 · f0.
To znamená, že pokud jsou tóny od sebe vzdáleny o jednu oktávu (oktáva – z latiny octo = osm, tedy osm celých tónů) neboli 12 půltónů, pak frekvence vyššího tónu je právě dvojnásobná oproti tónu nižšímu.
2. Realizace v Matlabu
2.1. Získání signálu
Celý průběh demonstrace úlohy je řízen ze souboru index.m:
% Konstanty
fs = 44100; % Vzorkovaci frekvence [Hz]
zv=0.5; % Koeficient zpetne vazby [-]
delka=0.5; % Delka zaznamu [s]
delkavz=delka*fs;% Delka zaznamu [vzorku]
dl=round(fs*delay); % Prodleva [vzorku]
noty=[];
% Ziskani signalu
q='No';
while strcmp(q,'No')
x = getsample(delkavz,fs);
q=questdlg('Pokracovat dale ve zpracovani?');
end
% Zpracovani
%x=reverb(x,dl,zv);
q=questdlg('Demonstrace Tape delay');
soundsc(reverb(x,0.5*fs,0.1),fs);
% Zaznamenani chromaticke stupnice
q=questdlg('Zaznamenani chromaticke stupnice');
n=2;
chroma=chromaStupnice(x,n,fs);
% Prehrani pisnicky
q=questdlg('Prehrani pisnicky');
pisen=[1 5 8 1 5 8 5 5 3 5 6 3 5 5 3 5 6 3 5 3 1];
playSong(pisen,chroma,fs);
% Hra na klavir
klavir(chroma,fs);
Nejprve získáme signál, který chceme dále zpracovávat. K tomu slouží funkce getsample.m:
function y=getsample(delkavz,fs)
a=questdlg('Bude se nahravat vzorek. Pripraven?');
if strcmp(a,'Yes')
y = wavrecord(delkavz, fs, 'double');% Nahrani zaznamu
elseif strcmp(a,'No')
f=440;
t=1:delkavz;
y=sawtooth(2*pi*t*(f*(1+20*sin(2*pi*10/fs)))/fs,0.7); % Synteticky zvuk
y=y+sin(2*pi*t*50/fs);
y=normal(y');
end
figure(1);
subplot(221);
plot(y);
title('Vstupni zvukovy signal');
axis([0 delkavz -1 1]);
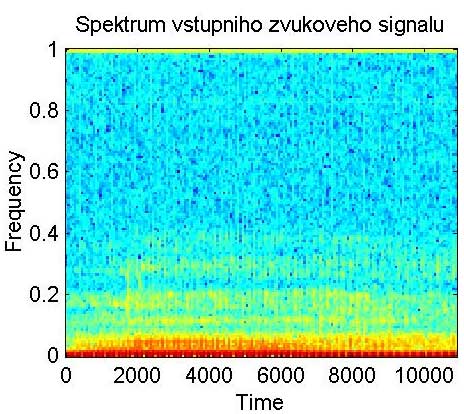
subplot(222);
specgram(y);
title('Spektrum vstupniho zvukoveho signalu');
wavplay(y, fs);
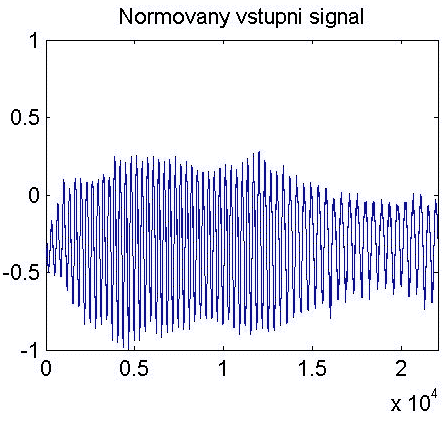
y = normal(y); % Normovani na 1
figure(1);
subplot(223);
plot(y);
axis([0 delkavz -1 1]);
title('Normovany vstupni signal');
subplot(224);
ffty=abs(fft(y));plot(ffty);
axis([0 delkavz/2 0 max(ffty)*0.75]);
title('Spektralni slozky vstupniho signalu');
wavplay(y, fs);
Pokud je k dispozici mikrofon, bude sejmut signál z mikrofonu. Pokud není k dispozici, funkce vytvoří vlastní syntetický zvuk.
Obr.5: Vstupní zvukový signál
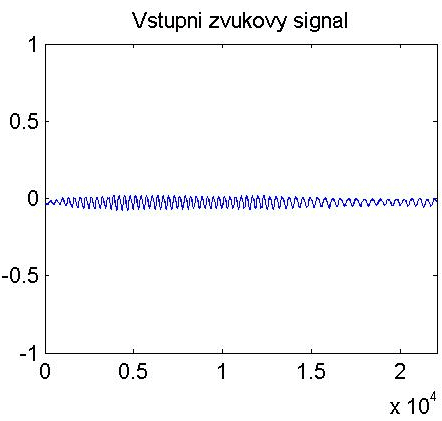
Protože signál z mikrofonu je poměrně slabý, je potřeba ho zesílit. Zároveň je tím normován na jednotkovou úroveň. K tomu slouží funkce normal.m:
% Normovani na jednotkovou uroven
function y=normal(x)
y = x/max(abs(x));
Jak je vidět, byla použita značně nekvalitní zvuková karta a ještě nekvalitnější mikrofon.
Obr.6: Normovaný vstupní signál
Ukážeme si ještě spektrum celého průběhu signálu (funkce specgram.m) …
Obr.7: Spektrum vstupního zvukového signálu
… a vykreslíme spektrální složky signálu (získané pomocí fft.m). Na obrázku je zvětšený detail zhruba do 700Hz.
Obr.8: Spektrální složky vstupního zvukového signálu
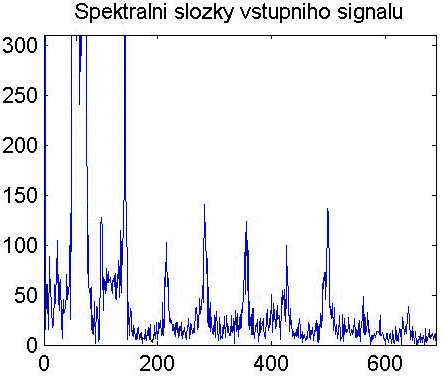
Nyní máme signál připravený k dalšímu zpracování.
2.2. Simulace efektu Tape Delay
Tento proces je simulován ve funkci reverb.m (název implikuje možnost budoucího rozšíření o další efekty):
% Funkce vraci signal prosly efektem Tape delay
% x ... puvodni vektor
% delay ... prodleva [pocet vzorku]
% zv ... koeficient zpetne vazby, 0<zv<1
function y=reverb(x,delay,zv)
tapeHeads=10;
de=length(x)+tapeHeads*delay;
figure(2);
for i=1:tapeHeads
y=x*zv; % Utlumeni
x=x*(1-zv); % Aby v souctu daly oba signaly 100%
x=[x;zeros(delay,1)]; % Srovnani delek
y=[zeros(delay,1);y];
x=x+y; % Zmixovani
mez=max(abs(x));
subplot(tapeHeads,1,i),plot(x),axis([1 de -mez mez]);
end
subplot(tapeHeads,1,1);
title('Demonstrace Tape Delay');
y=normal(x); % Navratovy vektor
Aby byl jev názorný, zvolili jsme počet deseti magnetofonových hlav. Princip spočívá v tom, že k signálu je ve smyčce přičítán stejný signál, ale zpožděný a zmenšený. Obrázek ukazuje, jak signál vypadá při průchodu každou hlavou.
Obr.9: Demonstrace Tape Delay
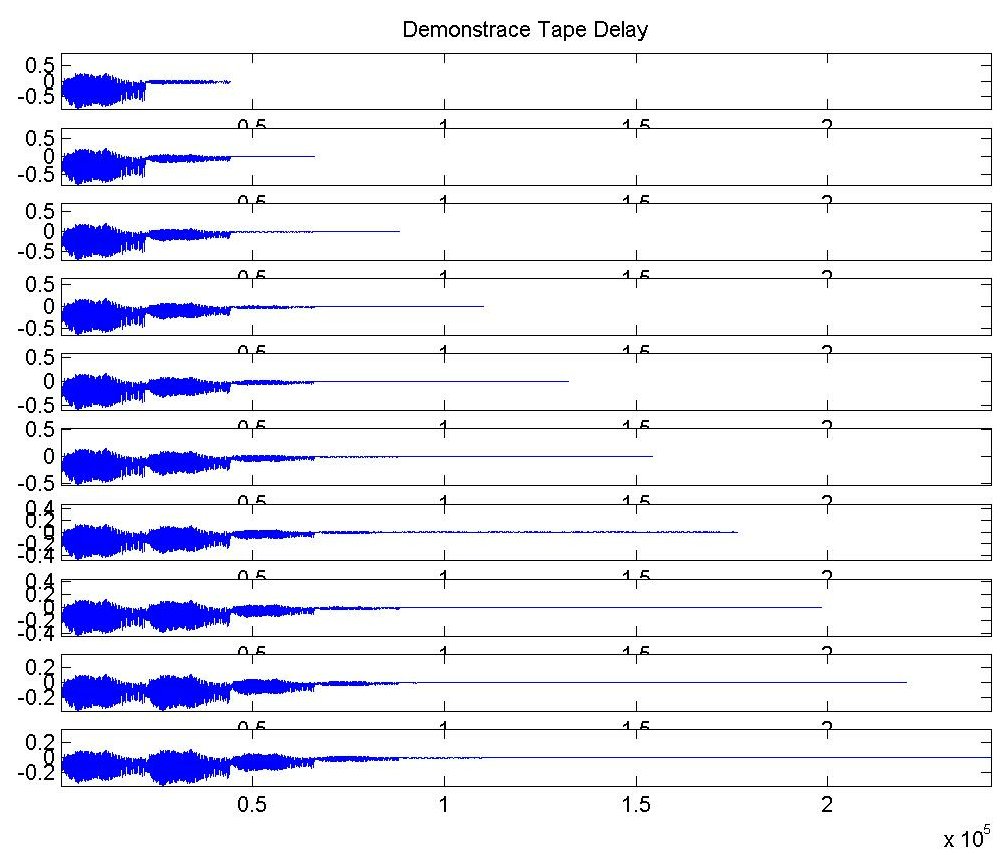
Nakonec je signál ještě normován na jednotkovou úroveň opět pomocí funkce normal.m (to už v obrázku není zakresleno).
2.3. Vytvoření chromatické stupnice
Vrátíme se k původnímu získanému a normovanému signálu a budeme zkoumat úlohu jeho převzorkování v neceločíselném poměru. Chceme z něj vytvořit chromatickou (půltónovou) stupnici v rozsahu jedné oktávy. K vytvoření koeficientů chromatické stupnice slouží funkce chromaCoef.m:
% Vytvoreni koeficientu chromaticke stupnice
function coef=chromaCoef(nic)
ton=2^(1/12);
for i=1:12
coef(i)=ton^(i-1);
end;
Její výstup vidíme na následujícím obrázku: geometrická řada dvanácti hodnot s kvocientem 12√2. Na první pohled se jen málo liší od lineární posloupnosti. Je zřejmé, že první člen musí mít hodnotu 1, třináctý člen řady by měl hodnotu přesně 2.
Obr.10: Koeficienty chromatické stupnice v rozsahu jedné oktávy
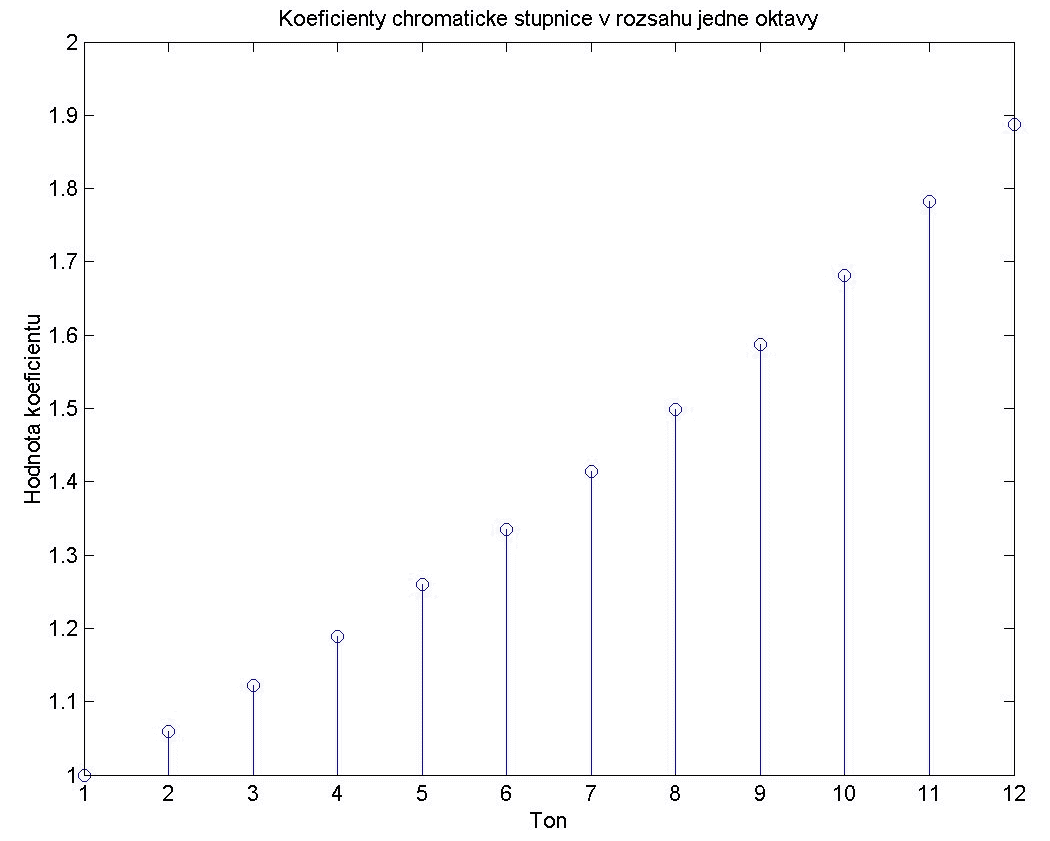
Když známe koeficienty frekvencí v chromatické stupnici, můžeme zavolat funkci chromaStupnice.m, která využívá právě popsané funkce chromaCoef.m a ze zadaného signálu nám vytvoří jednotlivé tóny chromatické stupnice.
% Zaznamenani chromaticke stupnice
% x ... zaznam, signal
% n ... rad resamplovani, napr. n=2 => 10na2 = 100
function chroma=chromaStupnice(x,n,fs)
coef=chromaCoef('');% Vytvoreni koeficientu stupnice
figure(3);
subplot(111);
stem(coef);
axis([1 12 1 2]);
title('Koeficienty chromaticke stupnice v rozsahu jedne oktavy');
xlabel('Ton');
ylabel('Hodnota koeficientu');
chroma=[,];
for i=1:12
nota=coef(i);
b=round(10^n); % tj. 100
a=round(b*nota); % <100;200)
q=resample(x,b,a);
%q=reverb(q,0.1*fs,0.03);
l=length(q);
%delka=l;% Nenecham to dlouhe
delka=min([l,fs*0.3]);
s=q(1:delka);
s=obalka(s);% Obalova krivka
soundsc(s,fs);
chroma(1:length(s),i)=s;
figure(4);
subplot(12,1,i);
plot(s);
axis([1 length(s) -1 1]);
end
subplot(12,1,1);
title('Prevzorkovany signal');
Její výsledek vidíme na následujícím obrázku:
Obr.11: Přrvzorkovaný signál
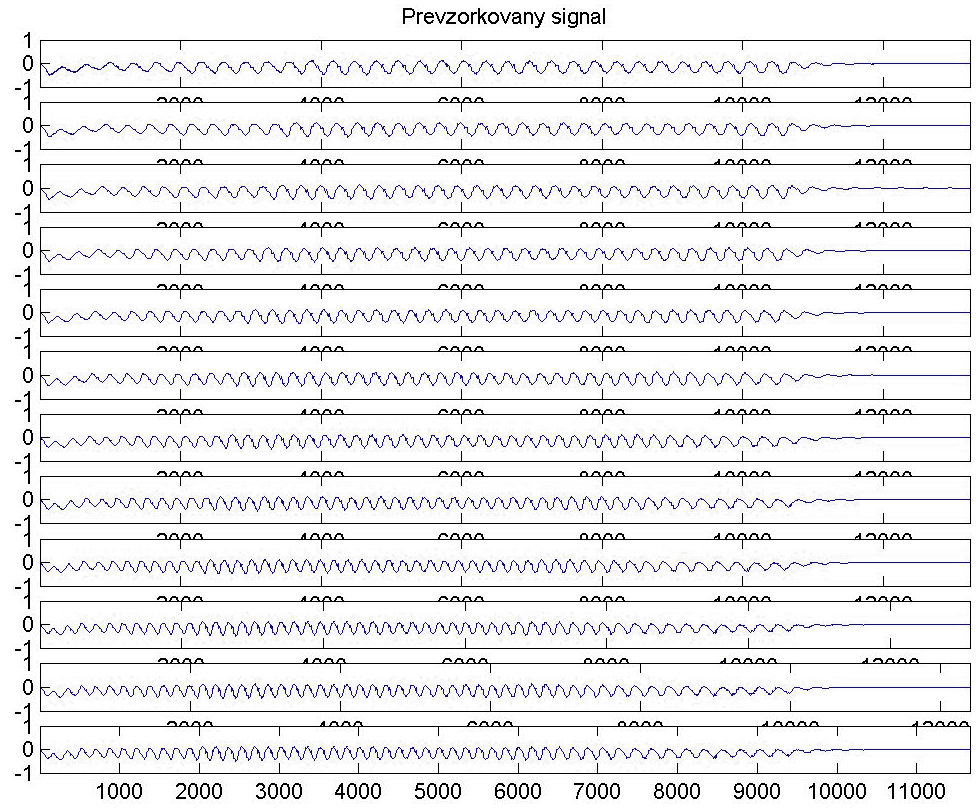
Tóny jsou zobrazeny od nejnižšího po nejvyšší. Můžeme pozorovat, jak se jednotlivé frekvence postupně „zahušťují“. Popišme si blíže tuto funkci.
Nejprve z funkce chromaCoef.m získáme koeficienty chromatické stupnice. Následuje cyklus, který zpracuje každý půltón jednotlivě: Provede se zaokrouhlení příslušného koeficientu s „rozumnou“ přesností. Zvolili jsme přesnost řádu n=2, neboli 102. To znamená, že funkce vypočítá celá čísla v řádu stovek a s nimi dále provede převzorkování původního signálu v neceločíselném poměru (např. 100 ku 189). Tím, že interpolační faktor je vždy menší nebo roven faktoru decimačnímu, výsledný efekt se jeví jako decimace. (Kromě první posloupnosti vzorků, která zůstane nezměněna).
Dále dojde ke zkrácení signálu tak, aby všechny půltóny měly stejnou délku.
Nakonec je danému signálu definována obalová křivka pomocí funkce obalka.m:
% Doda signalu obalovou krivku
function y=obalka(x)
x=x';% Aby se s nim lepe pracovalo
le=length(x);
ax=[0 le -1 1];
figure(5),subplot(211),plot(x),axis(ax);
% Delky
de1=round(le*0.01);% Nabeh
de2=round(le*0.05);% Pokles
de4=round(le*0.2); % Utlumeni
de3=le-de1-de2-de4;% Prubeh = zbytek
% Vahy
normalLevel=0.5;
va1=linspace(0,1,de1);
va2=linspace(1,normalLevel,de2);
va3=normalLevel*ones(1,de3);
va4=logspace(log10(normalLevel),-3,de4);
va=[va1 va2 va3 va4];
hold on;
figure(5),subplot(211),plot(va,'r'),axis(ax);
hold off;
title('Puvodni signal, obalova krivka');
y=x.*va;
y=y';% Zpet do sloupce
figure(5),subplot(212),plot(y),axis(ax);
title('Signal s definovanou obalkou');
Co tato funkce se signálem udělá, je zřejmé z obrázku:
Obr.12: Obalová křivka signálu
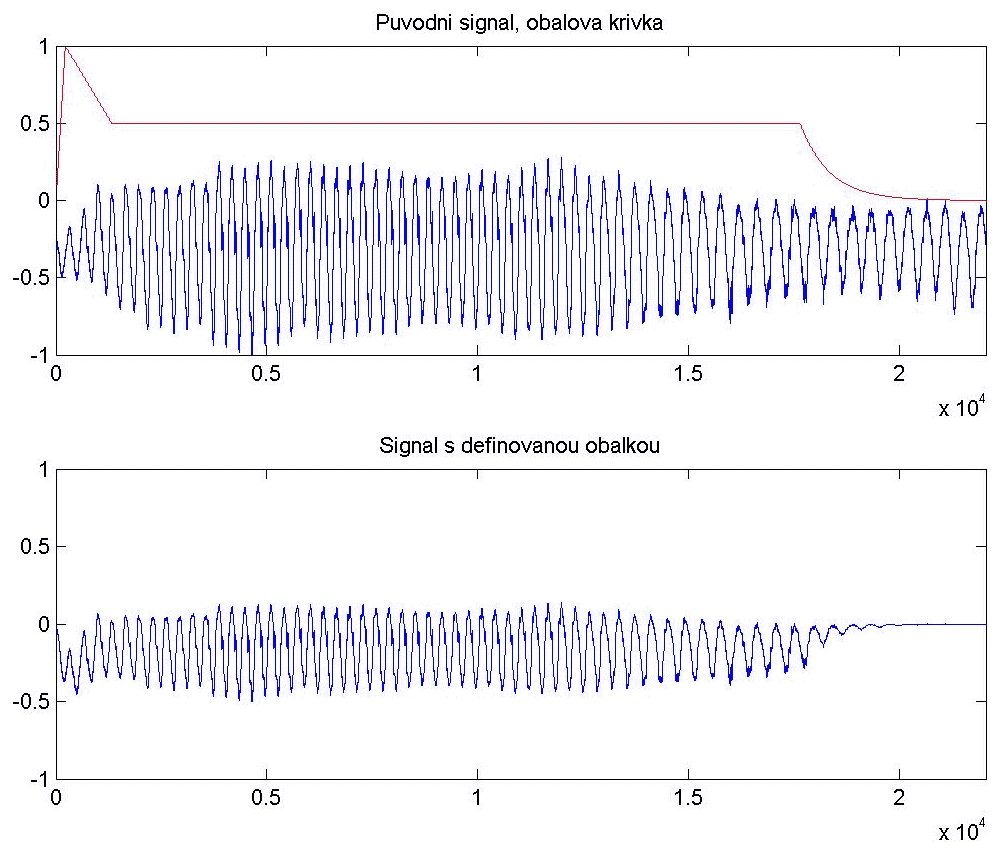
Jde v podstatě o váhování průběhu signálu. Po původním náběhu intenzity signálu a poklesu přichází ustálený průběh a nakonec dojde k jeho utlumení. Takto obecně můžeme charakterizovat veškeré zvuky, které se kolem nás vyskytují.
Nyní máme k dispozici celou stupnici včetně půltónů a můžeme vytvořeným zvukem přehrávat jednoduché skladby. To za nás dělá funkce playSong.m:
% Prehrani pisnicky
% pisen ... vektor, relativni vysky
% chroma ... matice, jednotlive chromaticke tony
% fs ... vzorkovaci frekvence
function playSong(pisen,chroma,fs)
for m=1:length(pisen)
i=pisen(m);
q=chroma(:,i);
wavplay(q,fs);
end
V konkrétním případě je funkci předána melodie písničky „Ovčáci, čtveráci“.
Na závěr, na vyzkoušení všech půltónů, i těch, které nezazněly ve skladbě, si je můžeme přehrát pomocí funkce klavir.m:
% Objevi se menu, stiskem jednotlivych polozek se prehravaji tony
function klavir(chroma,fs)
m=0;
while(m~=1) m=menu('Klavir','Konec','h1','b1','a1','g#1','g1','f#1','f1','e1','d#1','d1','c#1','c1');
nota=14-m;
if(nota<=12)
s=chroma(:,nota);
soundsc(s,fs);
else
for i=1:12
s=chroma(:,i);
wavplay(s,fs);
end
end
end
Podle stisknuté „klávesy“ funkce vybere příslušný vzorek a přehraje ho.
3. Literatura
[1] Uhlíř J., Sovka P., Čmejla R.: Úvod do číslicového zpracování signálů, Vydavatelství ČVUT, 2003
[2] Zaplatílek K., Doňar B.: Matlab pro začátečníky, BEN, Praha, 2003
[3] Vlachý V.: Praxe zvukové techniky, Muzikus, Praha
